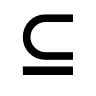زیرمجموعه یا برابر

	HTML	ﻢﻌﻨﯾ
⊂	⊂ ⊂ U+2282	زیرمجموعه (Subset) نماد زیرمجموعه که با ⊂ نمایش داده می‌شود، در نظریه مجموعه برای نشان دادن این استفاده می‌شود که یک مجموعه زیرمجموعه‌ای از مجموعه دیگری است، اما با آن برابر نیست.
⊆	⊆ ⊆ U+2286	زیرمجموعه یا برابر (Subset or Equal to) نماد زیرمجموعه یا برابر که با ⊆ نمایش داده می‌شود، نشان می‌دهد که یک مجموعه یا زیرمجموعه‌ای از مجموعه دیگری است یا با آن برابر است.
⊄	⊄ ⊄ U+2284	زیرمجموعه نیست از نماد زیرمجموعه نیست از، که با ⊄ نمایش داده می شود، نشان می دهد که یک مجموعه زیرمجموعه یک مجموعه دیگر نیست، به این ترتیب عدم شامل شدن را نشان می دهد.
⊈	⊈ U+2288	زیرمجموعه نیست یا برابر با نماد زیرمجموعه نیست یا برابر با، که با ⊈ نمایش داده می شود، نشان می دهد که یک مجموعه نه زیرمجموعه یک مجموعه دیگر است و نه با آن برابر است.
⊃	⊃ ⊃ U+2283	مجموعه بالایی (Superset) نماد مجموعه بالایی که با ⊃ نمایش داده می‌شود، برای نشان دادن این استفاده می‌شود که یک مجموعه مجموعه بالایی از مجموعه دیگری است، اما با آن برابر نیست.
⊇	⊇ ⊇ U+2287	مجموعه بالایی یا برابر (Superset or Equal to) نماد مجموعه بالایی یا برابر که با ⊇ نمایش داده می‌شود، نشان می‌دهد که یک مجموعه یا مجموعه بالایی از مجموعه دیگری است یا با آن برابر است.
∈	∈ ∈ U+2208	عضو مجموعه (Element of) نشان می‌دهد که یک شیء عضوی از یک مجموعه است.

نماد "زیرمجموعه" چیست؟

نماد زیرمجموعه که با ⊂ نمایش داده می‌شود، نشان می‌دهد که یک مجموعه داخلی در یک مجموعه دیگر وجود دارد، اما با آن برابر نیست. به عنوان مثال، اگر مجموعه‌های A = {1، 2، 3} و B = {1، 2، 3، 4، 5} داشته باشیم، می‌توان آن را به صورت A ⊂ B بیان کرد که بیانگر این است که A یک زیرمجموعه از B است.

نماد "زیرمجموعه یا برابر" چیست؟

نماد زیرمجموعه یا برابر که با ⊆ نمایش داده می‌شود، نشان می‌دهد که یک مجموعه یا زیرمجموعه‌ای از مجموعه دیگری است یا با آن برابر است. برای مجموعه‌های مشابه A و B، A ⊆ B نیز درست است زیرا A یک زیرمجموعه از B است. اما اگر A = {1، 2، 3} و B = {1، 2، 3} باشد، A ⊆ B به عنوان نماد مناسب است زیرا دو مجموعه برابر هستند.

تفاوت بین نمادهای زیرمجموعه

درک تفاوت بین دو نماد برای جلوگیری از ابهام بسیار مهم است. به یاد داشته باشید که ⊂ به معنای زیرمجموعه صرف (برابر نیست) است، در حالی که ⊆ به معنای زیرمجموعه یا برابر است. نماد آخر امکان دارد دو مجموعه مورد مقایسه با هم برابر باشند.

کاربردها و استفاده‌های منحصر به فرد نمادهای زیرمجموعه

نمادهای زیرمجموعه (⊂ و ⊆) در زمینه‌های ریاضی و محاسباتی مختلف کاربردهای مهمی دارند:

• نظریه مجموعه: برای بیان روابط بین مجموعه‌ها استفاده می‌شوند.
• ریاضیات: در زمینه‌های مختلف برای نشان دادن روابط مجموعه‌ها استفاده می‌شوند.
• علوم کامپیوتر: برای الگوریتم‌ها و ساختارهای داده برای بیان روابط و عملیات مجموعه استفاده می‌شوند.

تایپ کردن نمادهای زیرمجموعه

• ویندوز: برای ⊂ از Alt+8834 و برای ⊆ از Alt+8838 استفاده کنید.
• مک: به دسترسی به هر دو نماد از طریق نمایش دهنده کاراکتر دسترسی دارید.
• لینوکس: برای ⊂ از Ctrl+Shift+u سپس 2282 و برای ⊆ با 2286 پیروی کنید.
• HTML: برای ⊂ از ⊂ یا ⊂ و برای ⊆ از ⊆ یا ⊆ استفاده کنید.
• لاتک: برای ⊂ از \subset و برای ⊆ از \subseteq استفاده کنید.

تصاویر نمادها